Activitats sobre vectors en el pla
Moltes vegades el professorat de primer curs de Batxillerat es troba que l’alumnat procedent de l’ESO té uns nivells molt diferents de coneixements de la seva matèria i, per això, és interessant que hi hagi eines que puguin ajudar a establir uns nivells bàsics però uniformes, ja que constitueixen com una espècie de pont entre l’ESO i el Batxillerat. Aquest és el cas d’una aplicació anomenada “Activitats sobre vectors en el pla”, i que és obra de Jaume Bartrolí Brugués professor de l’IES Manuel Carrasco i Formiguera de Barcelona. Cal destacar que també té versions en castellà (versión en castellano) i en anglès (english version).
Per si la voleu utilitzar, convindria primer consultar el manual de l’aplicació, on hi trobareu les instruccions de funcionament tant pel profesorat com per l’alumnat, i després ja podeu passar a treballar qualsevol de les 5 unitats didàctiques de que consta, i en cadascuna de les quals hi ha 10 activitats diferents distribuïdes de la manera següent:
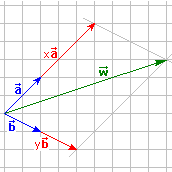
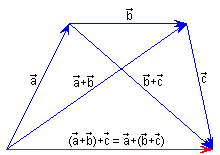
– Treballar amb vectors donats gràficament (fletxes): Vectors: mòdul, direcció i sentit, Suma de vectors, Commutativitat de la suma i Regla del paral·lelogram, Associativitat de la suma, Commutativitat de la suma de tres o més vectors, Sumes i restes de vectors, Producte d’un escalar per un vector, Combinacions lineals de dos vectors, Combinacions lineals de tres vectors, Distributivitat del producte respecte de la suma.
– Treballar amb vectors utilitzant coordenades i components: Components d’un vector, Suma de vectors utilitzant components, Regla del paral·lelogram, Associativitat de la suma, Commutativitat de la suma, Sumes i restes de vectors, Vectors i translacions, Vectors i forces; un exemple: un vaixell en un canal, Productes per escalars i combinacions lineals, Més sobre combinacions lineals.
– Mòduls i arguments. Vectors en forma polar: Mòdul d’un vector, Argument d’un vector, Vectors en forma polar (o en forma mòdul-argument), Mòdul del producte d’un escalar per un vector, Argument del producte d’un escalar per un vector, Mòdul de la suma de dos vectors, Obtenció de vectors de mòdul 1 (unitaris), Obtenció dels components coneguts el mòdul i l’argument, Obtenció del mòdul i de l’argument coneguts els components, Suma de dos vectors donats en forma polar.
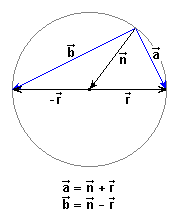
– Primeres aplicacions dels vectors a la geometria: Punt mitjà d’un segment, Simètric d’un punt respecte d’un altre punt, Divisió d’un segment en més de dues parts, Baricentre d’un triangle, Paral·lelisme de vectors, Alineació de punts, Sobre paral·lelograms, Introducció a les bases: la base canònica, Bases no canòniques, Bases no canòniques i obliqües.
– Producte escalar de dos vectors: Definició de producte escalar de dos vectors, Interpretació geomètrica del producte escalar, Propietats: commutativitat i associativitat respecte els escalars, Propietats: distributivitat respecte de la suma, Obtenció del producte escalar a partir dels components, Perpendicularitat de dos vectors, Cosinus de l’angle que formen dos vectors, Projecció d’un vector sobre un altre, Retrobem un teorema atribuït a Tales de Milet, Retrobem el teorema de Pitàgoras.